Page 124 - Vector Analysis

(b) On the sphere x2 + y2 + z2 = 9, the outward point normal vector n (x, y, z) = 1 (x, y, z).
3

Therefore, by (0.1) (with f (x, y, z) = 3yez in mind),

y2ezdS = 3yez y dS = ∂ (3yez )dV = 3 2π π
3 ∂y
120 Σ Σ D 3eρ cos φρ2 sin φdφdθdρ

3 2π φ=π C0 HA0PTER0 4. Vector Calculus

= 3 −ρeρ cos φ dθdρ
φ=0
Example 4.51. Let C b0e a3 0smooth by
curve parameterized

= 6π (ρeρ − ρe−ρ)dρ

0 ρ=t3 P [π π]
´2, .
r=(t6)π=(ρ(−cos1t)esρinρt=,3si−n t6sπi(n−t,ρc−os1t))e,−ρ ρ=0
ρ=0 2

= 12π(e3 + 2e−3) . []

The clearly C is on the unit sphere S2 since }r(t)}R3 = 1 for all t P ´ π , π . Since C is a
2 2
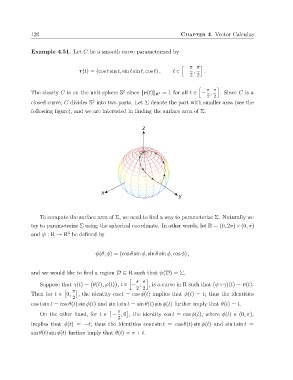
Probclloesmed 5c.urLveet, CC dbieviadesms So2otihntcoutrwveo ppaarratms. eLtreitzeΣd dbeynote the part with smaller area (see the

following figure), an⇀rd (wt)e=ar(ecoinsttesrienstte, dsinint sfiinndti,ncgostth)e, surfa−ceπ2a≤reat o≤f Σπ2..

z

xy

1. (10%) Show that the corresponding curve of ⇀r (t) on θφ-plane consists of two line segments L1
To compute the surface area of Σ, we need to find a way to parameterize Σ. Naturally we
and Lp2argaimveentebryize Σ using the spherical coordinate. In other words, let R = (0, 2π) ˆ (0, π)
try to

and ψ : R ÑL1R=3 be(θd,eφfi)neθd=byφ , 0 ≤ φ ≤ π , L2 = (θ, φ) θ = π − φ,0 ≤ φ ≤ π .
2 2

2. (10%) Plot L1 and L2 onψ(tθh,eϕθ)φ=-p(lcaonseθ. sTinhϕe, csuinrvθesiCn ϕd,icvoisdϕes) ,the unit sphere into two parts,
and let Σ be the part with smaller area. Identify the corresponding region of Σ on θφ-plane.

3.an(1d5w%e) wFoinudldtlhikeesutorfaficnedaareraegoifonΣ.D Ď R such that ψ(D) = Σ.
[ ]
() ´ π π ,
Suppose that γ(t) = θ(t), φ(t) , t P 2 , 2 is a curve in R such that (ψ ˝ γ)(t) = r(t).
[ ] implies that ϕ(t) = t; thus the identities
Then for t P 0, π , the identity cos t = cos ϕ(t)

2

cos t sin t = cos θ(t) sin ϕ(t) and sin t sin t = sin θ(t) sin ϕ(t) further imply that θ(t) = t.

On the other hand, for t P [ ´ π , ] the identity cos t = cos ϕ(t), where ϕ(t) P (0, π),
2 0,

implies that ϕ(t) = ´t; thus the identities cos t sin t = cos θ(t) sin ϕ(t) and sin t sin t =

sin θ(t) sin ϕ(t) further imply that θ(t) = π + t.