Page 151 - Vector Analysis

§4.7 The Stokes Theorem 147

As in Example 4.51 and Example 4.88, we would like to find the area of Σ, and verify
the Stokes theorem for the special case that F : R3 Ñ R3 given by

F(x, y, z) = (y, ´x, 0) .

To find the surface area of Σ, we need to parameterize Σ. As in Example 4.51, we look
( ) ()
for γ(t) = θ(t), ϕ(t) , t P [0, 2π], such that ψ γ(t) = r(t), where ψ : R ” (0, 2π) ˆ (0, π) is

given by ψ(θ, ϕ) = (cos θ sin ϕ, sin θ sin ϕ, cos ϕ) .

For t P (0, π), since cos t = cos ϕ(t) and ϕ(t) P (0, π), we must have ϕ(t) = t; thus the

two identities cos(sin t) sin t = cos θ(t) sin ϕ(t) and sin(sin t) sin t = sin θ(t) sin ϕ(t) further
()

imply that θ(t) = sin t. Therefore, the curve r (0, π) corresponds to θ = sin ϕ, ϕ P (0, π),

on R.

On the other hand, for t P (π, 2π), the identity cos ϕ(t) = cos t implies that ϕ(t) = 2π ´

t. The two identities cos(sin t) sin t = cos θ(t) sin ϕ(t) and sin(sin t) sin t = sin θ(t) sin ϕ(t)

further imply that

cos(sin t) = ´ cos θ(t) and sin(sin t) = ´ sin θ(t) t P (π, 2π) .
()

Therefore, θ(t) = π + sin t which implies that the curve r (π, 2π) corresponds to θ =
π ´ sin ϕ, ϕ P (0, π), on R.

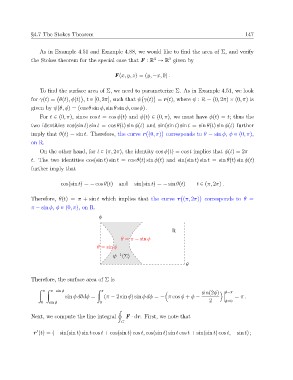
ϕ

θ = π ´ sin ϕ R
θ = sin ϕ θ

ψ´1(Σ)

Therefore, the surface area of Σ is

żπ ż π´sin ϕ sin ϕ dθdϕ = żπ ´ 2 sin ϕ) sin ϕ dϕ = ( cos ϕ + ϕ ´ sin(2ϕ) )ˇϕ=π = π .
(π ´π ˇ
0 sin ϕ
0 2 ˇϕ=0

¿

Next, we compute the line integral F ¨ dr. First, we note that

C

r 1(t) = (´ sin(sin t) sin t cos t + cos(sin t) cos t, cos(sin t) sin t cos t + sin(sin t) cos t, ´ sin t) ;