Page 132 - Vector Analysis

128 CHAPTER 4. Vector Calculus

Such a normal vector fields is said to be compatible with the parametrization tV, ψu. To be
more precise, we have the following

Definition 4.62. Let Σ Ď R3 be an oriented C 1-surface, and N : Σ Ñ R3 be a continuous

unit normal vector field of Σ. For each p P V, N is said to be compatible with a local
parametrization tV, ψu of Σ at ( 1 ... ψ,2 ... )
p if det [ψ, N ˝ ψ] ą 0.

The following example provides a famous regular surface which is not oriented.

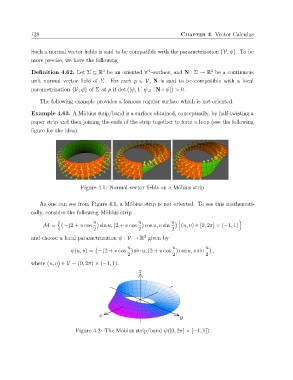
Example 4.63. A Möbius strip/band is a surface obtained, conceptually, by half-twisting a
paper strip and then joining the ends of the strip together to form a loop (see the following
figure for the idea).

Figure 4.1: Normal vector fields on a Möbius strip

As one can see from Figure 4.1, a Möbius strip is not oriented. To see this mathemati-

cally, consider the following Möbius strip

M = !( + v cos u ) sin u, (2 + v cos u ) cos u, v sin u ) ˇ (u, v) P [0, 2π] ˆ (´1, )
´(2 2 2 2 ˇ 1)
ˇ

and choose a local parametrization ψ : V Ñ R3 given by

ψ(u, v) = ( + v cos u) sin u, (2 + v cos u ) cos u, v sin u) ,
´(2 2
2 2

where (u, v) P V ” (0, 2π) ˆ (´1, 1).

z

xy
Figure 4.2: The Möbius strip/band ψ([0, 2π] ˆ [´1, 1])